Linear Hashing^2,3 is a hash table algorithm suitable for secondary storage. It is often used to implement hash indices in databases and file systems. Linear Hashing was invented by Witold Litwin in 1980 and has been in widespread use since that time. I implemented this file-structure earlier this year. You can find my implementation on github. This article is based off a talk¹ I gave at CWRU Hacker Society.

I also implemented an in memory version of this algorithm. I give a detailed break down of each element of the implementation in the follow up post. You should read that article after you have finished this one.

Hashing, A Refresher

In order to understand Linear Hashing one should take a moment to review Classical Hashing.⁴ Briefly, a hash table is a "symbol table" which maps keys to values. By "maps" I mean if you give it a key it will give the associated value if one exists. Keys must be hashable, which means there must be some way to turn them into integers. For a discussion on constructing such hash functions I recommend the Hashing Tutorial.⁴

Abstract Data Type

If the above description was confusing perhaps this ADT will clarify what I mean:

HashTable
  size():int -- how many entries?
  has(key:Hashable):boolean -- is the key in the table?
  get(key:Hashable):Object throws KeyNotFound -- get the associated value.
  put(key:Hashable, value:Object) -- associate a key and value.


  remove(key:Hashable) throws KeyNotFound -- remove the key from the table.

Hashable
  hash():int

You may have used hash tables by another name in you programming language. For instance in Python they are called dictionaries, in Ruby hashs, and in Java they are called HashMaps.

Implementation

Let's walk through a simple hash table implementation using separate chaining (also called open hashing). We will do this in the Go programming language.

Structs

Here is how we are going to represent a hash table:

type Hashable interface {
    Equals(b Hashable) bool
    Hash() int
}

type entry struct {
    key Hashable


    value interface{}
    next *entry
}

type hash struct {
    table []*entry


    size int
}

A hash is a struct with to elements. An array of pointers to entry. The entries hold our key value pairs. The way the table works is we convert the key into a number which we then clamp to the size of our table. That number will be the index of some entry in our table from which we can add, lookup, or remove the key.

The entry struct represents the key value pair and represents a linked list. Since covering linked list operations is a bit beyond the scope of this paper, let me just present operations on the *entry but with no explanation. The function should be obvious even if the implementation is obscure.

func (self *entry) Put(key Hashable, value interface{}) (e *entry, appended bool) {
    if self == nil {
        return &entry{key, value, nil}, true
    }
    if self.key.Equals(key) {
        self.value = value
        return self, false
    } else {
        self.next, appended = self.next.Put(key, value)
        return self, appended
    }
}

func (self *entry) Get(key Hashable) (has bool, value interface{}) {
    if self == nil {
        return false, nil
    } else if self.key.Equals(key) {
        return true, self.value
    } else {
        return self.next.Get(key)
    }
}



func (self *entry) Remove(key Hashable) *entry {
    if self == nil {
        panic(Errors["list-not-found"])
    }
    if self.key.Equals(key) {
        return self.next
    } else {
        self.next = self.next.Remove(key)
        return self
    }
}

Operations on the Hash Table

Now for how to implement the different operations. As a reminder we are going to convert our key to an index into the table as our first step. Let's make a function for that and call it bucket

func (self *hash) bucket(key Hashable) int {


    return key.Hash() % len(self.table)
}

Insertion

Putting an object into a hash table is very simple. We grab the bucket and use the associate Put method to place our key value pair into the list. If it was actually appended onto the list (rather than updating and existing entry) we increment the size field.

func (self *hash) Put(key Hashable, value interface{}) (err error) {
    bucket := self.bucket(key)
    var appended bool


    self.table[bucket], appended = self.table[bucket].Put(key, value)
    if appended {
        self.size += 1
    }
}

Now there is one more wrinkle I will return to in a moment which is resizing the table when it gets too full.

Retrieval

Retrieval is just as easy. We grab the bucket and look in the linked list to see if it is there or not. If it is, return it.

func (self *hash) Get(key Hashable) (value interface{}, err error) {
    bucket := self.bucket(key)
    if has, value := self.table[bucket].Get(key); has {
        return value, nil
    } else {
        return nil, Errors["not-found"]
    }
}

Removal

Removal is almost the same as insertion except we call Remove on the linked list instead of Put and update the head as before. We check to make sure it is in the linked list first as this slightly simplifies the removal algorithm above.

func (self *hash) Remove(key Hashable) (value interface{}, err error) {
    bucket := self.bucket(key)
    has, value := self.table[bucket].Get(key)

    if !has {
        return nil, Errors["not-found"]
    }
    self.table[bucket] = self.table[bucket].Remove(key)
    self.size -= 1
    return value, nil
}

Expansion

The performance of a hash table degrades as it gets too full. Therefore, we have to periodically expand the size of the hash table. As long we double the size each time all of our operations are asymptotically linear (on average). To double the size of the table, we allocate a new table and copy all of the entries from the old table to the new. We must be careful when we do this and rehash each element. If we don't, we will be unable to find the elements in the new table since the bucket function depends on the table size.

func (self *hash) expand() error {
    table := self.table

    self.table = make([]*entry, len(table)*2)
    self.size = 0
    for _, E := range table {
        for e := E; e != nil; e = e.next {
            if err := self.Put(e.key, e.value); err != nil {
                return err
            }
        }
    }
    return nil
}

Insert Revisited

So when should we expand the hash table? We should expand on insert when the number of elements is over a certain threshold. The threshold is often set at 60% but this setting varies.

func (self *hash) Put(key Hashable, value interface{}) (err error) {
    bucket := self.bucket(key)
    var appended bool
    self.table[bucket], appended = self.table[bucket].Put(key, value)
    if appended {
        self.size += 1
    }
    if self.size * 2 > len(self.table) {
        return self.expand()
    }
    return nil
}

Adapting Hash Tables for Secondary Storage

Figure 1. CPU and Storage

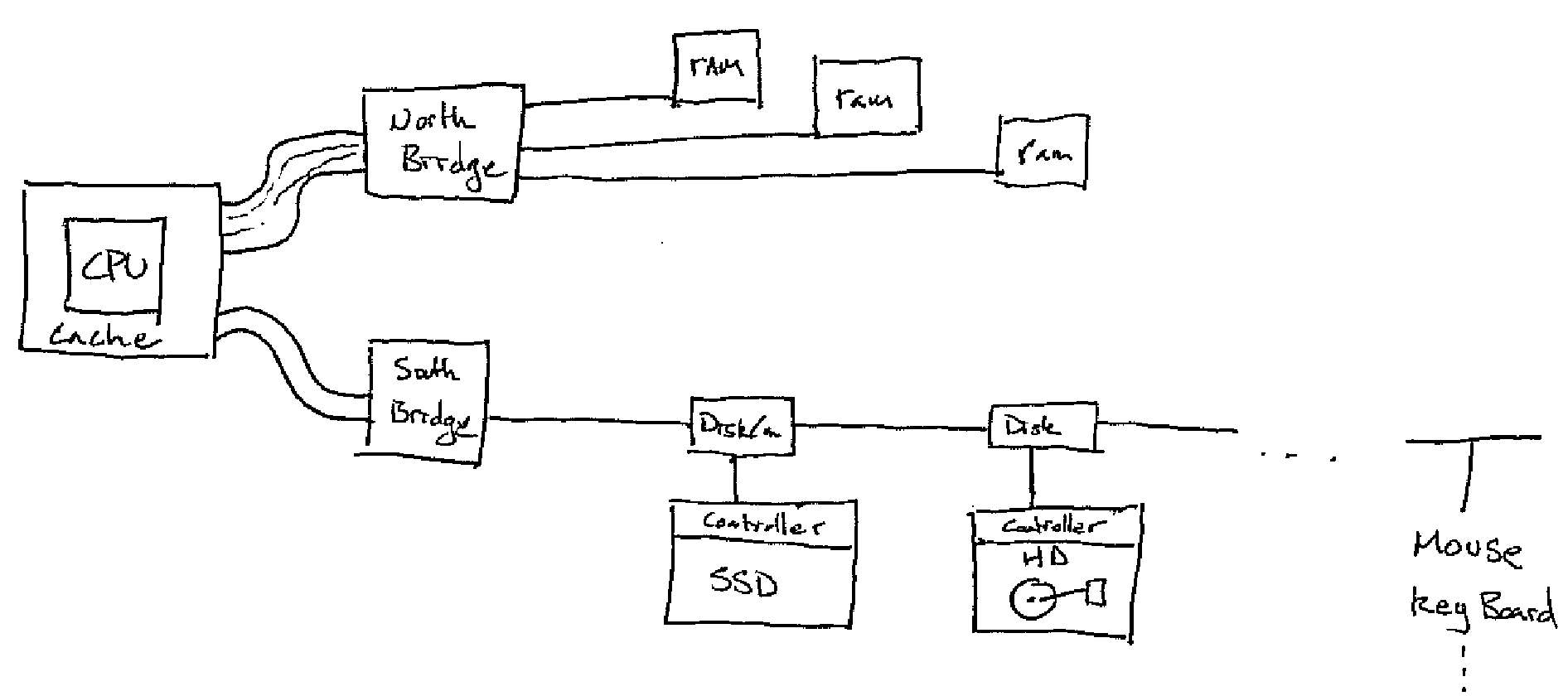
Unfortunately, the algorithm presented above does work well when using secondary storage mediums like hard disks and solid state drives. There are several reasons for this:

1. Secondary Storage is slower than RAM
2. The bus is slower
3. Many peripherals hang off of the South Bridge
4. Disks may be daisy chained causing bus contention

To deal with these factors and others when using disks:

1. Read and write pages which are blocks of size 4096 bytes.
2. Try and read contiguous runs and if writing more than one page write contiguous runs as well.
3. Batch writes.
4. Don't read one byte at a time, read several blocks and get the byte that you need.
5. Employ caching at every layer.
6. Measure performance in terms of number of disk accesses (eg. Block read and writes).

Back to Hashing

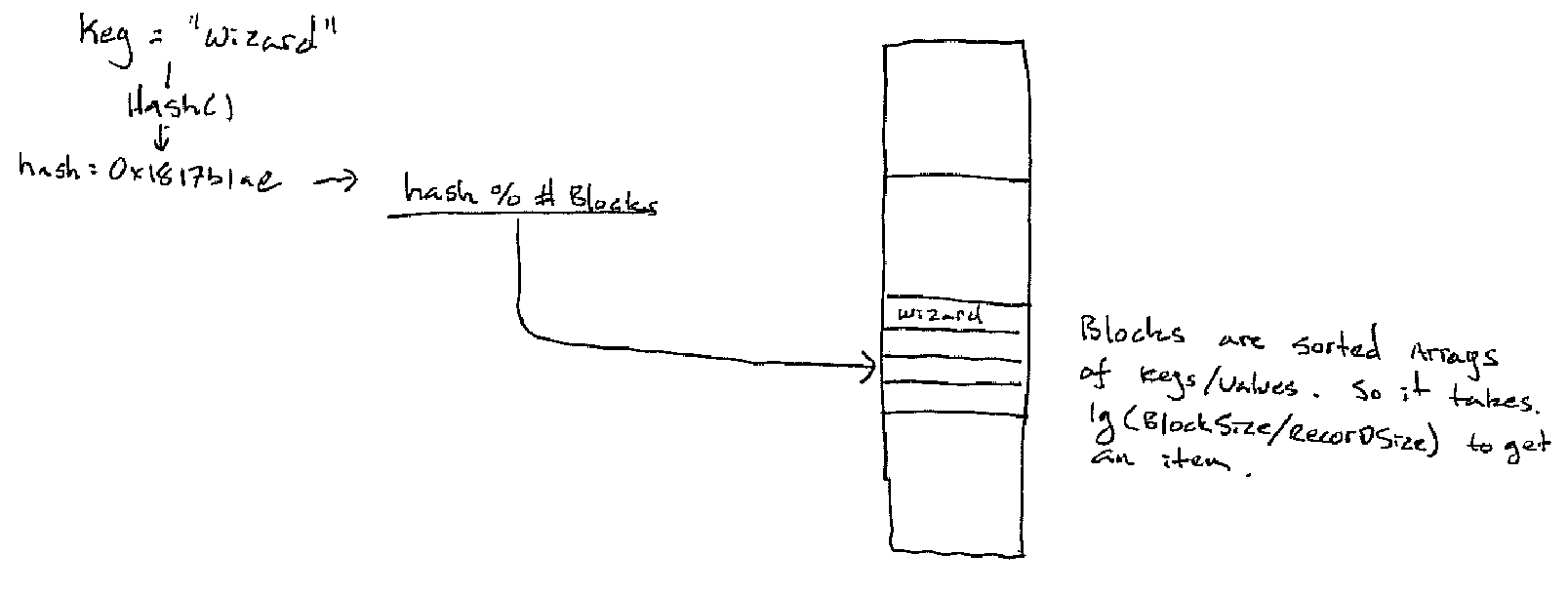
The first adjustment to make is to hash into blocks instead of hashing into individual array buckets. Each block is then a sorted array of entries.

Figure 2. Block File

We could make a fairly straight forward adaption of our separate chained hash table above to this restriction. However, there is a problem: what do we do when the table needs to be expanded? If the table is static then there is not problem, we simply allocate the correct number of blocks right away. But, if we have to expand the table every entry will need to be rehashed. This will cause us to read from every block from our old table (N reads) and write to every block in our new table (2*N writes) -- ouch.

The solution is of course Linear Hashing.

Linear Hashing

How does Linear Hashing compare?

1. Small mean disk accesses
   1. Successful Search
      1. .75 utilization ~ 1.05 disk accesses
      2. .9 utilization ~ 1.35 disk accesses
   2. Unsuccessful Search
      1. .75 utilization ~ 1.27 disk accesses
      2. .9 utilization ~ 2.37 disk accesses
   3. Insert
      1. .75 utilization ~ 2.62 disk accesses
      2. .9 utilization ~ 3.73 disk accesses

2. In comparison a B+Tree of reasonable size might need at least 4 disk access for a search. (Of course a B+Tree will can perform range queries but that isn't the point here)

3. File grows at a linear rate.

4. Little dynamic re-arrangement

5. Does not necessarily need address translation.

6. Simple Algorithm esp. in comparison to B+Trees.

Explanation of the Algorithm

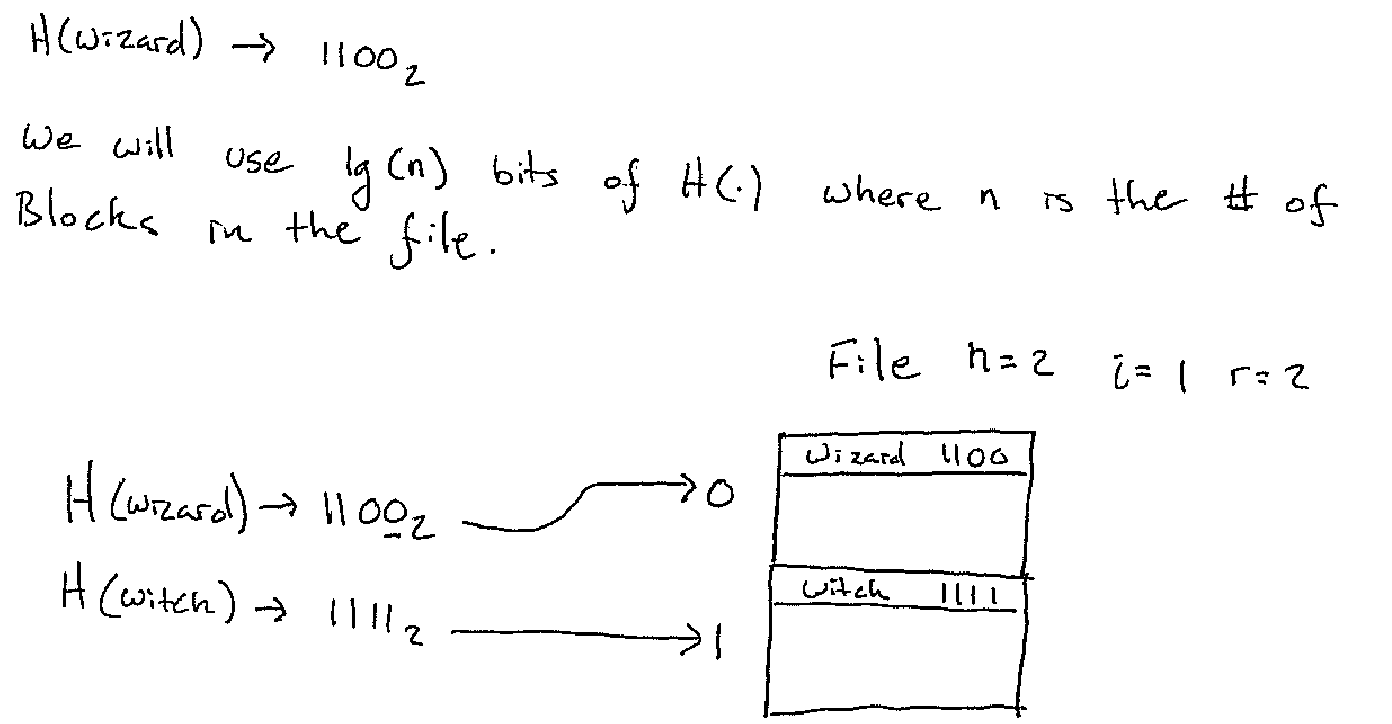
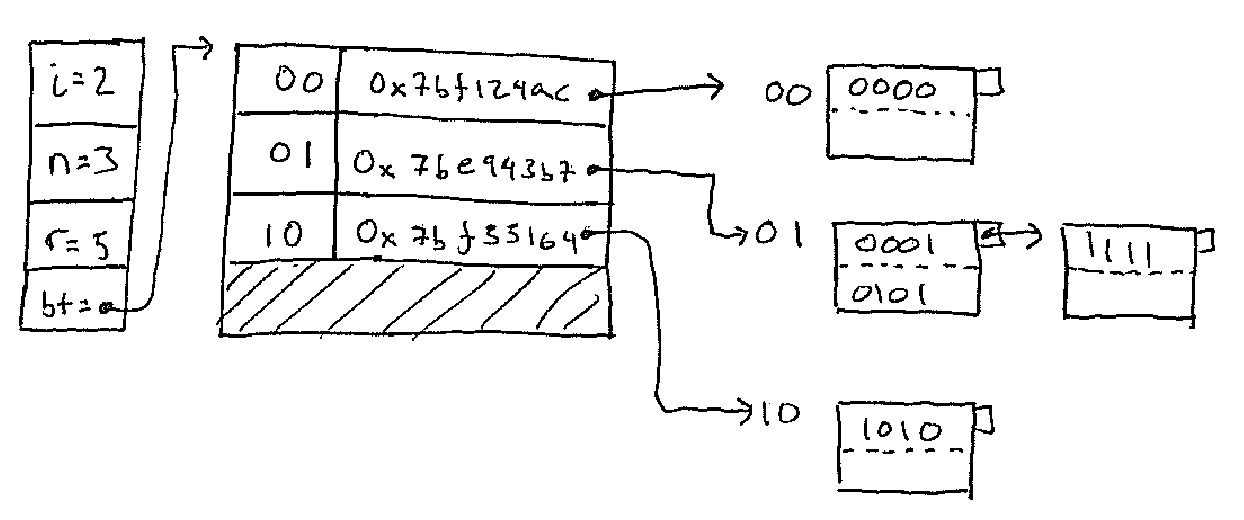
The key insight is to not use all the bits of the hash function "H(.)" all the time. When the table is small we only use as much of the hash function as we need. As the table grows we use more bits. As the table shrinks we use less.

Figure 3. Example

In the figure, n is the number of blocks, i is the number of bits of the hash functions and r is the number of records.

So to find which bucket a key goes to:

bkt_idx = let
  hash = x x x x a_1 a_2 ... a_i (* base 2 expansion of the hash of the key *)
  m = a_1 a_2 ... a_i (* just the first i bits *)
in
  if m < n then
    m
  else
    m - 2^(i-1) (* == 0 a_2 a_3 ... a_i *)
end

In go

func bucket(hash uint) uint {
    m := hash & ((1<<i)-1) // last i bits of hash as
                           // bucket number m
    if m < n {
        return m
    } else {
        return m ^ (1<<(i-1)) // unset the top bit
    }
}

Insertion

Insertion is quite simple now that we know how to get the bucket (assuming we have implemented the appropriate operations on our buckets). First we get the bucket and we put the item into the bucket. If the bucket takes care of chaining on an extra block if it full then the only thing that is left is checking whether or not an expansion (called a split) is needed.

func (self LinearHash) Insert(key Hashable, value []byte) error {
    hash := key.Hash()
    bkt_idx := self.bucket(hash)
    bkt := self.get_bucket(bkt_idx)
    if err := bkt.Put(key,value); err != nil {
        return err
    }
    self.r += 1
    if r > UTILIZATION * self.n * (self.records_per_block) {
        return self.split()
    }
    return nil
}

As I mentioned above, if a bucket is full it should chain out an extra block for itself. This can be handled transparently.

Figure 4. Chaining Example

Splitting

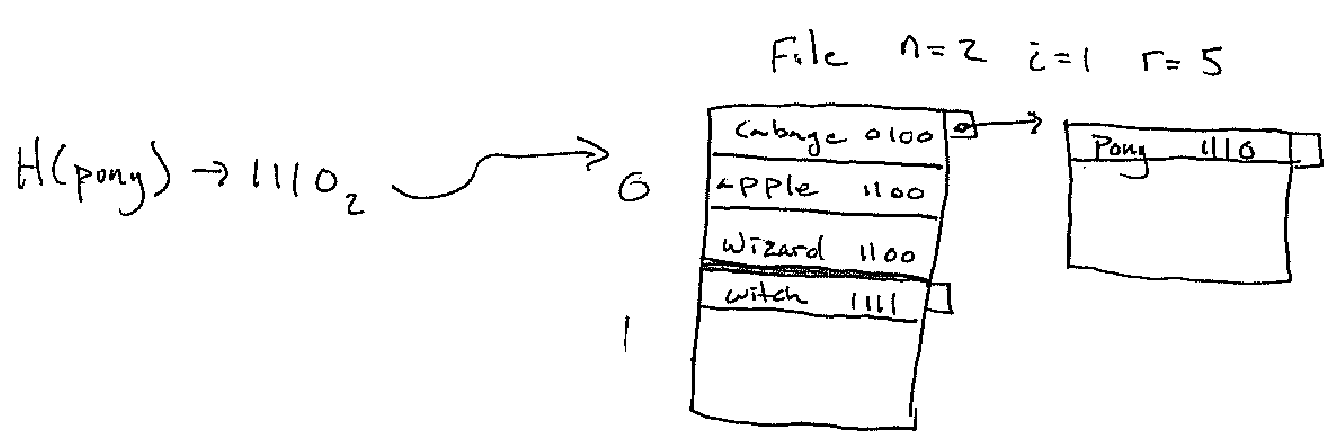
The split mechanism is clever bit of the linear hash algorithm. When the table is too full another block is added to the table:

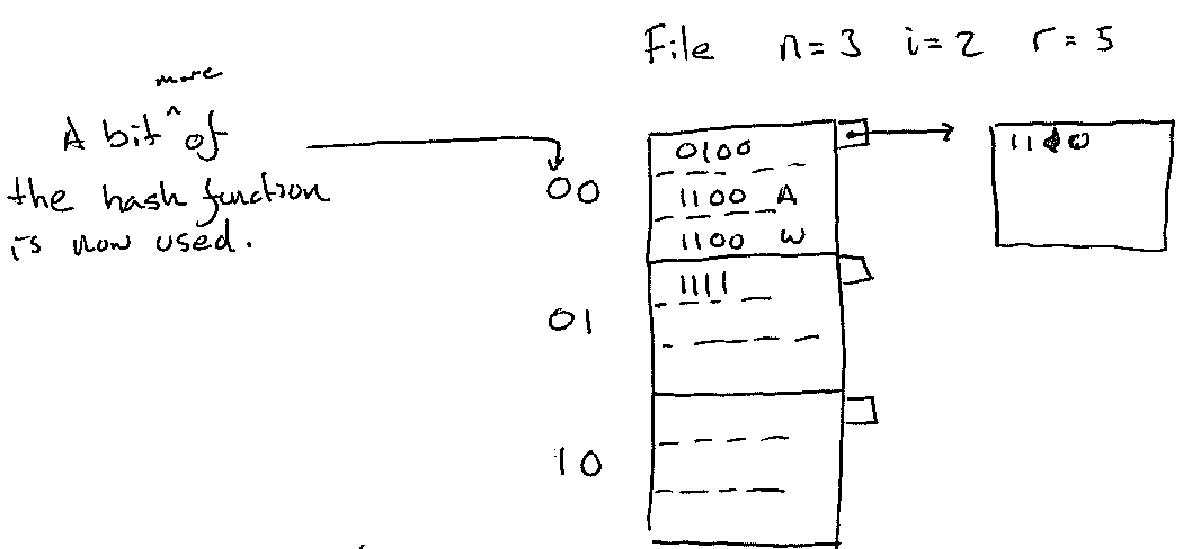Figure 5. Split Example Part 1

Note that the bucket we added in the example was

1 a_i == 1 0 == a_1 a_2

There are some keys in the old bucket 0 which is now called 00 which actually belong to bucket 10. So in order to make the addition of the new bucket correct we need to split bucket 00.

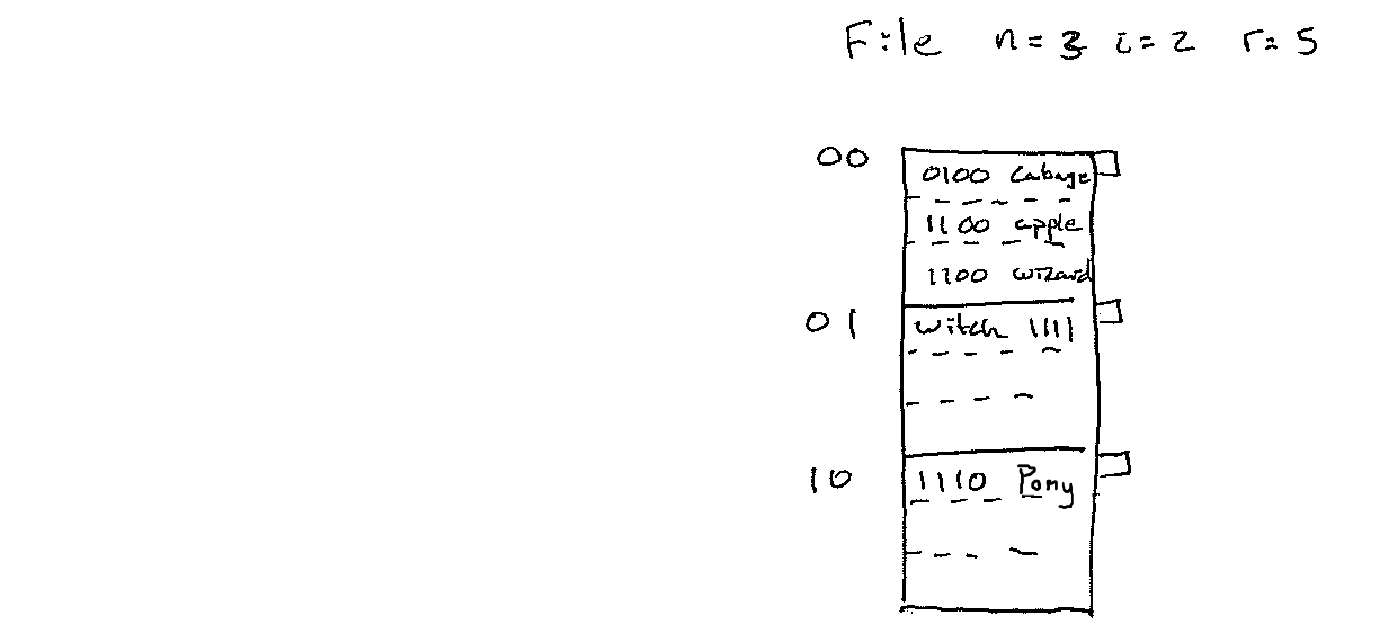Figure 5. Split Example Part 2

In general if we add

1 a_2 a_3 ... a_i

We split

0 a_2 a_3 ... a_i

In code⁵

func (self LinearHash) split() error {
    bkt_idx := self.n % (1 << (self.i - 1))
    bkt_a := self.get_bucket(bkt_idx)
    bkt_b, err := self.allocate()
    if err != nil {
        return err
    }
    self.n += 1
    if n > (1 << i) {
        self.i += 1
    }
    return blk_a.split_into(bkt_b)
    // The split into function is left as
    // an exercise for the reader!
}

Conclusion

Hopefully if you are still with me you have a grasp on what is going on in the Linear Hashing algorithm. The key take aways are:

1. You can slowly extend how much of the hash function you use.
2. You don't have to rehash the whole file to add a bucket, just the bucket that collides with the new bucket.

If you want to implement the algorithm I suggest reading the description in the Garcia-Molina book and taking a look at the original paper. You can also take a look at my implementation or my other implementation, an in memory version.