Searching a large corpus of strings is a problem many applications have to solve, whether the application features autocomplete boxes or full-text search. Efficient methods for conducting such searches are not always readily apparent to the algorithm designer. In this series of articles I will present a data structure known as the Ternary Search Trie (TST) which is designed to assist in solving this problem. For this introductory article I will not discuss algorithms in detail but only provide a high level overview of the structure and algorithmic running time for various operations. In the next article I will detail the process of maintaining the structure with insertions and deletions. The final article will discuss different flexible search algorithms and their implementations.

Symbol Tables: A Short Review

A symbol table is a mapping between a string key and a value which can be any type of object from an integer to a complex nested structure. There are two classic symbol table implementations most programmers are immediately familiar with: Binary Search Trees (BSTs) and hash tables. Both of these structures work by exactly matching the search key to the keys stored in the structure. If there does not exist an exact match then there is a miss. Thus, neither of these structures can serve as useful index for an autocomplete algorithm where only part of the key is known. They may be useful for a full text index, but they will not be as efficient as some of the other structures we will later discuss.

While these simple structures are limited, other symbol table implementations have properties more suited for modification for flexible string search. This series will focus on the Trie category of structures. These structures are more suited for partial match as we will see. But first, why are hash tables not suited for this job? They have such excellent running time characteristics, O(1) lookups! However, one cannot modify the hash table algorithm to effectively serve the purpose of a partial match or a range query. Why? Because hash functions transform strings into numbers (which correspond to buckets in an array). Good hash functions have wide variance in hashing strings and will not hash a similar string or a sub string to the same bucket.

Introducing the Trie

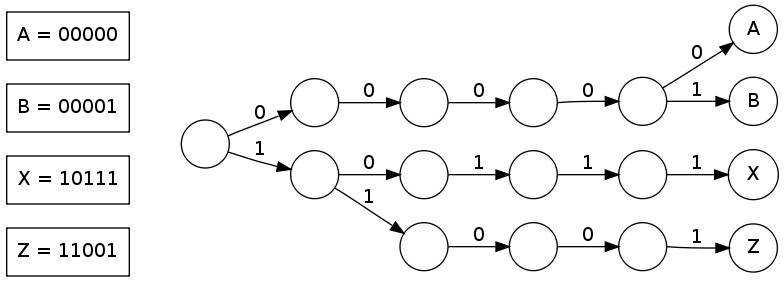
Figure 1. An Example Binary Search Trie

In general a Trie is a special for of a tree. However, instead of comparing entire key at each node during traversal, it only compares parts of keys. The key/value pairs are kept in the leaves (like in a B+ Tree). We will first consider a Binary Search Trie. Like the Binary Search Tree, each node in the Trie has two children, left and right. The left child is defined as the 0'' child and the right as the 1'' child. As a key is inserted, a node is created or visited for each bit in the key. When visiting a node which already exists, the direction to descend is based on the current bit. that is:

• let there be a function bit(i, s) which returns the ith bit in the string s.
• let depth(r, n) return the depth of the node n in the tree rooted at r
• bit(depth(r, n), s) is the bit in the string used to make the decision on which of n's children to visit.

Sedgewick gives the formal definition: "A [binary search] trie is a binary tree that has keys associated with each of its leaves, defined recursively as follows: The trie for an empty set of keys is a null link; the trie for a single key is a leaf containing that key; and the trie for a set of keys of cardinality greater than one is an internal node with left link referring to the trie for the keys whose initial bit is 0 and right link referring to the trie for the keys whose initial bit is 1, with the leading bit considered to be removed for the purpose of constructing the subtrees."¹

A search using this structure is directed by the strings in the database. However, since only one bit is considered at a time in the search for a k-bit string the search will take in the worst case k bit comparisons. This makes for a very tall structure when using string keys, since single characters will be at least 8 bits long in ASCII and much longer in Unicode. Another unfortunate implementation detail is that modern processors typically work more efficiently when accessing bytes or words. Thus, a more efficient structure might consider multiple bits at once.

Multi-way Tries

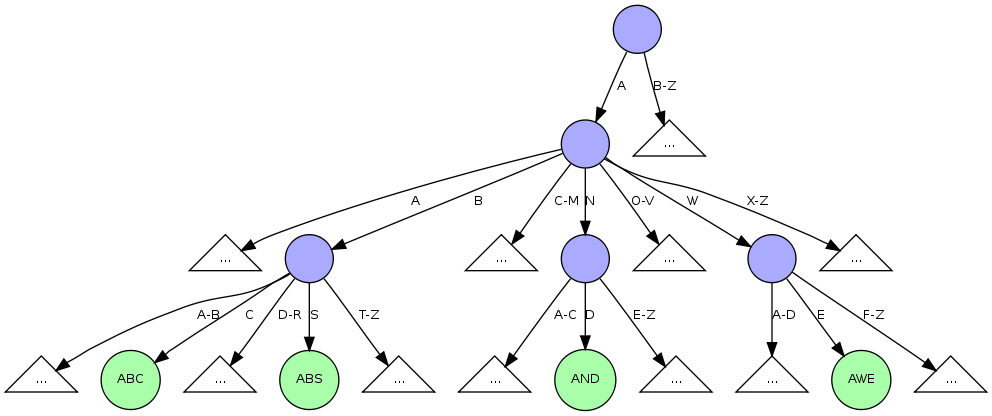
Figure 2. An Example R-Way Trie

If one considers multiple bits at once one has to increase the fanout (number of children per node) of the tree. Consider figure 2, in which each node has a fanout of 26.² While useful if every node has 26 children, the space to store the pointers becomes wasteful for real data. However, despite the wasted space in comparison to the binary version, searches on the R-Way Trie will perform faster than on the Binary Trie. It will be faster for the CPU to compare the bytes under consideration and there will be fewer comparisons over all. In general, a Binary Trie will require log~2~(N) comparisons to perform a search, and an R-way Trie it will take log~R~(N) comparisons.

However, to produce a usable structure for our purpose (a large in-memory string index) we need to cut down on the space wasted by the extra pointers in each node. The tricky bit is to do this while still maintaining the hard-fought gains in search speed. Simply using a dynamic structure like a hash table in each node to hold the array won't work either because hash tables are slower than an array access and if the hash table becomes overly full it may actually use more space than the array. Thus, a different structure is needed.

Ternary Search Tries

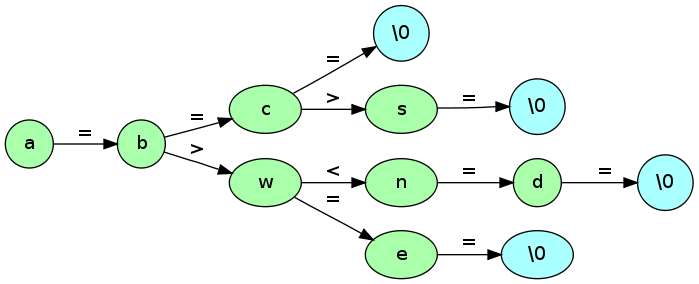
Figure 3. An Example Ternary Search Trie with strings [abc, abs, awe, and].

The Ternary Search Trie helps avoid the unnecessary space needed by a traditional multi-way trie while still maintaining many of its advantages. In a Ternary Search Trie each node contains a character and three pointers. The pointers correspond to the current character under consideration being less than, greater than or equal to the character held by the node. In a sense this structure is like taking the Multi-way Trie and encoding it on to a Binary Search Tree with the keys as current character and the values as another BST corresponding to the next character.

While a Multi-way Trie has about R*N/log~2~(R) pointers, a Ternary Search Trie has R + c*N pointers where c is a small constant, perhaps 3. Consider the graph of their performance:

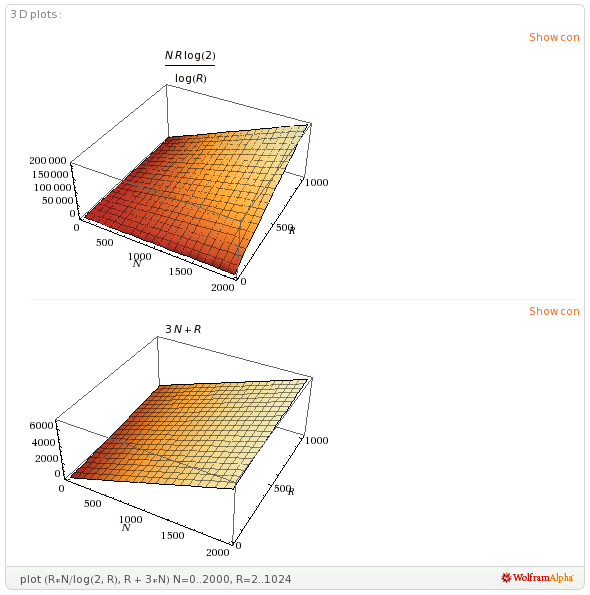
Figure 4. Links in a Multi-way Trie vs. a Ternary Search Trie

When R is small, 2, 3, 4 Multi-way Tries and Ternary Tries have similar a similar number of pointers, but a low branching factor destroys the advantage of the Multi-way Trie. When R grows to a larger, more reasonable size such as 256, the number of pointers explodes in comparison to the Ternary Trie. Thus, the Ternary formulation will be far more space efficient in the worst case than the Multi-way formulation.

What is the cost for better space efficiency? In the Multi-way Trie we must traverse at most the length of the search key links. In a TST we may need to traverse up to 3 times that many links in the worst case. However, this pathological case is rare. In the average case the situation can be made much better through a few small improvements to the basic structure.

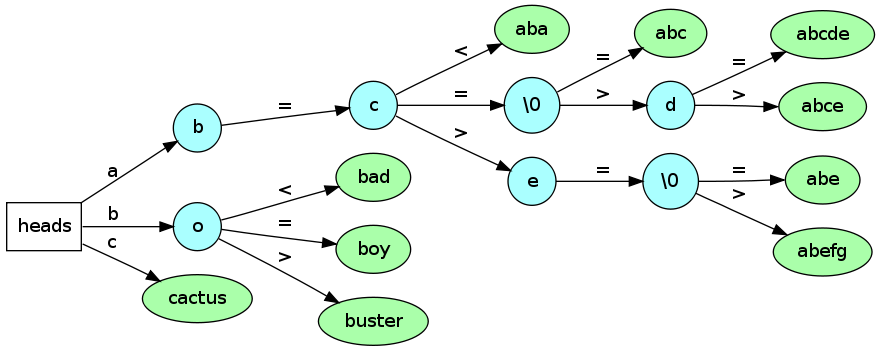
Figure 5. An Improved Ternary Search Trie.

The first improvement, illustrated below in Figure 5, involves collapsing the leaf nodes. Instead of allowing long chains of nodes at the leaves, we collapse them into a single node. This allows the final check to be computed efficiently.

The second improvement, also illustrated in Figure 5, combines the best of the Multi-way Search Trie with the Ternary Search Trie. The root node is an R-Way node like in the Multi-way Search Trie. The rest of the tree is a Ternary Search Trie with the leaf nodes collapsed. In practice these improvements result in an enormous speedup. The theory also supports the practice; according to Sedgewick, these improvements cut the number of comparisons needed in half.³

There is one final improvement to consider not shown the above figure. Similar to the first improvement, it involves collapsing nodes, but instead of collapsing leaf nodes, internal nodes are collapsed. This idea is similar to the Patricia Trie. When a group of strings shares the same contiguous substring, instead of having a node for each character shared, collapse the shared nodes into a single node.

Conclusion and Whats Next

In this post we discussed the theory behind Symbol Tables and the use of Tries as a symbol table implementation. The Trie, and in particular the TST, is an efficient way to implement a symbol table. A good implementation of a TST has comparable performance to a Hash Table.

You can puruse my Go (golang) implementation in my data-structures repository. I also wrote a python implementation.